广义线性模型GLM学习笔记

第一章：导论

• 定量变量可以叫做协变量，定性变量叫做因子。
• 因子需要进行数字化编码才能用在统计模型中，转换后叫做伪变量。
• 因子有n个水平时，伪变量至少需要n-1个。
• 合适的模型的标准：简单和准确。

第二章：线性回归模型

简介与回顾

• 线性回归模型是广义线性模型的一种特殊形式。

线性回归模型的定义

$$\begin{cases} var[y_i] = \frac{\sigma^2}{w_i}\\ \mu_i = \beta_0 + \sum_{j=1}^{p}\beta_jX_{ji} \end{cases}$$

在上面这个公式中：

• $y_i$表示的是第i个响应变量，也就是第i个因变量；
• $\sigma^2$表示的是$y_i$的方差；
• $w_i$表示的先验权重，是已知的，比如观测值的数量，比如100个观测值里面，30个观测值都是一样的，这时候30就可以作为先验权重，通常来说一个观测值只会出现一次，所以呢这个先验权重都是1如果出现的次数大于一次，就不再是1了；
• $\beta_0$到$\beta_p$都需要从数据中进行推断，也就是未知的；

• $\beta_o$通常被叫做截距（inercept），也就是当所有的自主变量都为0的适量，因变量所对应的值；$\beta_1$到$\beta_p$被称为斜率（slope）。

• 当只有一个自变量，也就是p = 1的时候，所得到的模型就是简单线性回归模型或者是简单回归模型；当p > 1的时候，就是多元回归模型，或者是多元线性回归模型。

• 当所有的先验权重都等于1的时候，就叫做普通回归模型；当所有的先验权重都不全是1的时候，就叫做加权的回归模型。

建模时需要满足的假设：

• 适用性：相同的回归模型适用于所有观测值；
• 线性：$\mu$和所有的定量变量之间的真实关系是线性的；
• 独立性：响应变量y是恒定的。

简单的线性回归

最小二乘估计

先看公式：

$$\begin{cases} var[y_i] = \frac{\sigma^2}{w_i}\\ \mu_i = \beta_0 + \beta_1x_{i} \end{cases}$$

简单线性回归的公式主要的部分是第二部分。

当我们给定一个$\beta_0$和一个$\beta_1$后，对每一个自变量，都可以得到一个模型计算后的理论观测值$\mu_i$. 既然是模型预测的，那肯定和实际的观测值有差异，我们可以用$e_i$来表示这个差异：

$$e_i= y_i- \mu_i = y_i - \beta_0 - \beta_1x_i$$

其实建模的过程就是找到合适的$\beta_0$和$\beta_1$，使得$e_i$最小。

为了避免有负值的出现，常见的做法是对其进行平方：

$$S(\beta_0,\beta_1) = \sum_{i=1}^{n}w_ie_{i}^2=\sum_{i=1}^{n}w_i(y_i-\mu_i)^2=\sum_{i=1}^{n}w_i(y_i-\beta_0-\beta_1x_i)^2$$

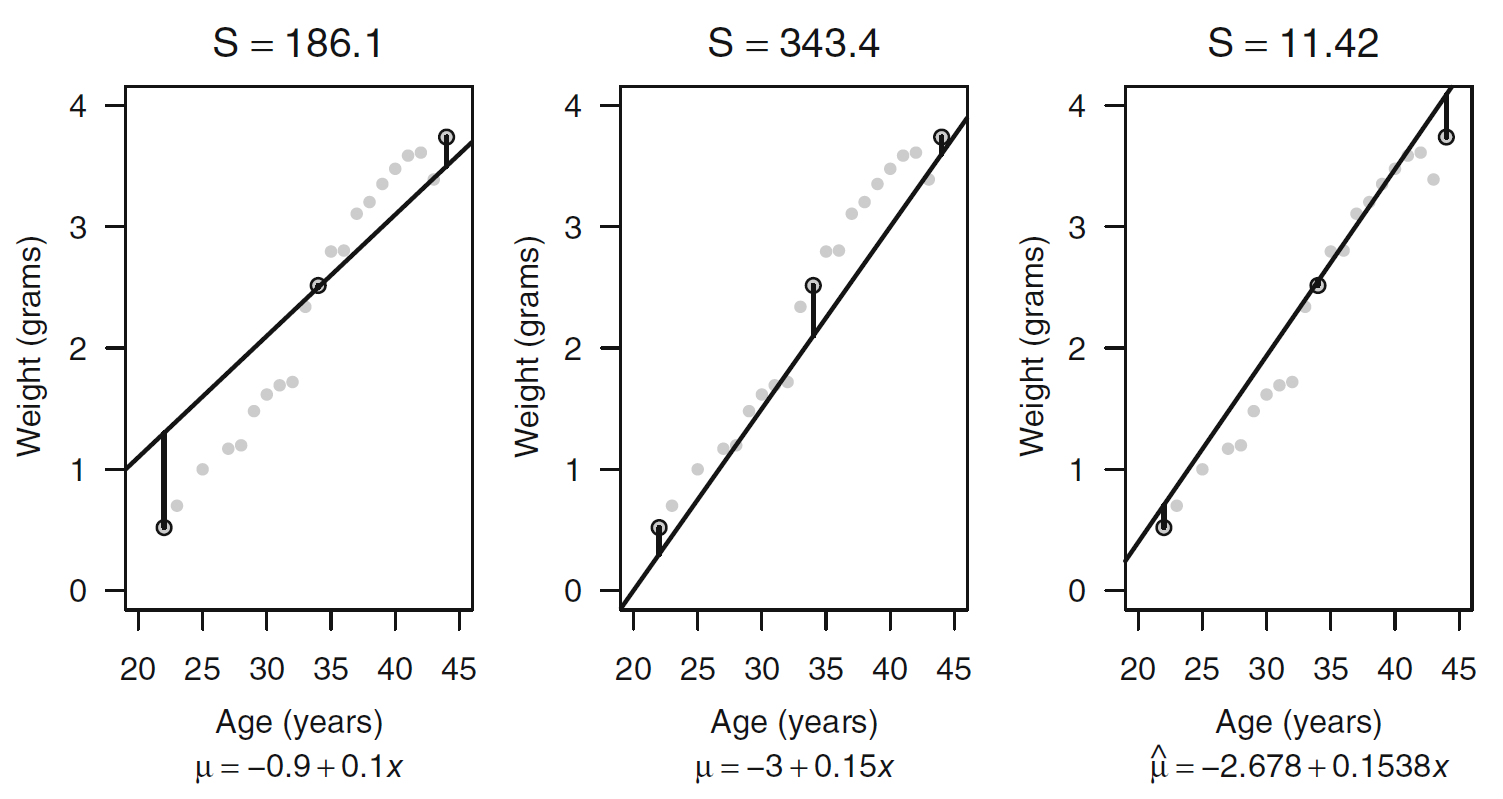
当S越小的时候，说明拟合的线到观测值的距离的和最小，也就是拟合得到的那根线基本可以代表自变量x和因变量y的真实关系。

系数估计

现在的问题是怎么找到最适的$\beta_0$和$\beta_1$?

$$S(\beta_0,\beta_1) = \sum_{i=1}^{n}w_ie_{i}^2=\sum_{i=1}^{n}w_i(y_i-\mu_i)^2=\sum_{i=1}^{n}w_i(y_i-\beta_0-\beta_1x_i)^2$$

一个方法就是使用微积分计算得到最小的$S(\beta_0,\beta_1)$.

$$\frac{\varphi S(\beta_0,\beta_1)}{\varphi \beta_0}=2\sum_{i=1}^{n}w_i(y_i-\mu_i)$$ $$\frac{\varphi S(\beta_0,\beta_1)}{\varphi \beta_1}=2\sum_{i=1}^{n}w_ix_i(y_i-\mu_i)$$