广义线性混合模型操作指南
更新版本:
推荐的资料
- https://bookdown.org/roback/bookdown-BeyondMLR/ch-GLMM.html
- https://m-clark.github.io/mixed-models-with-R/
文献信息
固定效应和随机效应
案例:假设有5种动物,每种动物测量了100只(指标是体重),得到500个数据点。
代码:
1 | |
控制数据点之间的非独立性
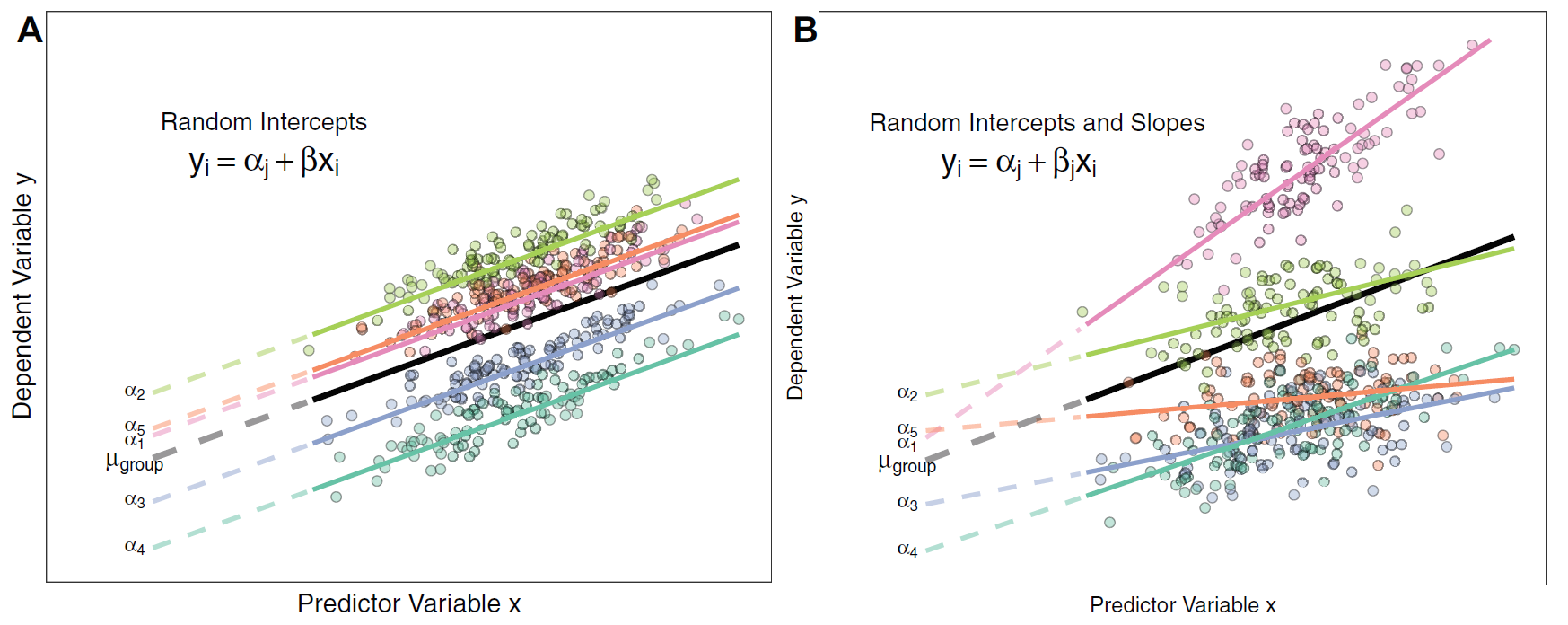
生物学数据通常是嵌套的,或者是具有层次结构的,比如多年多点多处理的重复测量数据。随机效应可以通过控制斜率或者是截距来控制这种非独立性。只拟合随机截距能够保证组件的均值是有差异的,但是得假设对一个拟合的协变量(固定效应)来说所有分组间的斜率是一样的。拟合随机截距和斜率允许预测变量的斜率根据单独的分组变量而变化。比如我们假设动物成功繁殖是其体重的一个函数,研究是说动物能否成功繁殖和其体重相关。如果有多点的采样,那么就会希望将“采样点”拟合为随机截距,然后去估计一个固定的斜率。也就是说成功繁殖“1单位”的变化在各组之间引起的变化是一样的。
1 | |
如果假设不同采样点会影响到繁殖率,也就是说不同采样点之间,体重对繁殖率的影响强度是不一样的(斜率不一样),即体重每改变 1 个单位,繁殖成功率的变化在各组之间并不一致。这时候就需要随机斜率。
1 | |
下面的图就分别展示了随机截距模型(A)和随机斜率且随机截距模型(B)。
提高参数估计的准确性
随机效应模型使用来自所有分组的数据来估计分组均值整体分布的均值和方差。**假设所有均值都来自于一个共同的分布,会导致均值的估计值向着全局均值漂移。这种现象叫收缩,可以得到更小更精确的均值标准误。
方差分量估计
有时候组间方差是被关注的。
拟合随机效应时的注意事项
- 拟合随机截距时,至少需要5个
level,也就是5个分组。 - 组间样本量差异较大时,模型很可能不稳定,尤其是随机斜率模型时。
- 难以评估组间方差的显著性和重要性。
- 随机效应的错误指定:
- 未能辨别嵌套数据中由于分层引起的非独立性,如对一只鸟多个窝点的测量;
- 没有指定随机斜率;
- 在分层模型的错误 “水平 “上测试固定效应的显著性。传统的方法是
F检验,但是呢F检验有缺陷,最新的标准方法是likelihood ratio tests,也就是似然比检验。
GLMM模型的结构
选择误差结构和链接函数
非正态的数据怎么处理:
- 转换成正态的再进行处理;
- 使用GLM或者是GLMM并指定合适的误差分布和链接函数,选用的链接函数考虑到了我们的数据的(假定的)经验分布。
直接的数据转换和通过链接函数得到的数据是不一样的,就是取对数的后的数和logarithm拟合后得到的新数据是不一样的。
选择随机效应
交叉还是嵌套?
实际数据可以根据试验设计或者是采样设计来指定随机效应。
下面的内容是旧的,部分描述可能不正确。
文献信息
关键名词
- 贝叶斯统计:一种统计学派或者说统计方法,特点是利用先验信息,形成先验分布,提高推断准确率。
- 偏差:估计值和真实值得之间的差异。
- 块随机效应:对组内所有个体影响一致的效应,导致群体内单一水平的相关性;
- 指数族:统计分布族,包括正态分布、二项分布、泊松分布、指数分布和伽马分布等。
- 固定效应和随机效应:固定效应和随机效应的区别就在于如何看待参数。对于固定效应来说,参数的含义是,自变量每变化一个单位,应变量平均变化多少。而对于随机效应而言,参数是服从正态分布的一个随机变量,也就是说对于两个不同的自变量的值,对应变量的影响不一定是相同的。
前言内容
- 当随机效应存在时,GLMM(Generalized linear mixed models,广义线性混合模型,广义线混模型)更适用于非正态的数据。
- 基础统计的一个基础是数据必须符合正态分布,而且呢基础统计想要量化的是每个变量的确切影响,也就是每个变量对目标变量的影响到底有多大。
- 一个很常见的随机效应:多年多点试验中的“区块”,可以理解成田间试验中的小区;个体之间的差异也可以看作随机效应。
- 在面对非正态分布的数据时,一种常见的取巧的办法是将非正态的数据转化为正态的,比如利用非参数检验。这些方法可能会忽视掉随机因子,或者是把这些随机因子当成了固定因子。
- 相比较于直接把数据丢进基础统计这个大框中,研究人员更应该考虑并选择合适的统计方法来满足他们的数据需求。
- GLMM融合了LMM和GLM两种模型的优势:LMM模型考虑了随机效应;GLM使用链接函数和指数族来处理非正态分布的数据。
- GLMM是处理非正态分布的最佳工具,在使用时只需要指定随机效应的分布、链接函数和结构。
估计Estimation
对大多数的统计分析来说,估计模型的参数是很重要的一步。对GLMM,主要的参数有两个:
- 固定效应参数:协变量的影响,处理和互作之间的差异。
- 随机效应参数:随机效应的标准差。
当前的大都数GLMM工具都是利用最大似然法(Maximun Likelihood,ML)来估计这些参数的。如果,试验设计的时候的均衡的,响应变量是正态的,所有的处理都有一样的样品量,所有的随机效应都是嵌套效应,那么这时候用ANOVA计算得到的参数和ML计算得到的参数是一致的。但是对于更复杂的LMM或者是GLMM,就没有那么简单了:要找到ML的估计值,就需要对随机效应所有的ML估计值进行整合,这种方法呢就比较慢,而且当数据量大的时候,可能会计算不了。
为了解决这些问题,统计学家开发出伪似然等方法来估计GLMM的参数。需要区分标准的最大似然法(假定固定效应的估计值是准确无误的,然后去估计随机效应的标准差)和有限的最大似然法(REML)(对固定效应中的某些不确定进行平均化)。在数据集不是很大的时候,ML会低估随机效应的标准差;但是对于具有不同固定效应的模型,ML更有用。
penalized quasilikelihood(PQL)是最简单的,也是使用最广泛的。但是当司机效应的标准差过大时,PQL会得到有偏的参数,尤其是在处理二进制数据时。Poisso分布数据的平均Counts小于5或者是二进制数据中成功/失败的平均期望值小于5时,PQL的表现会比较差,但是还是有很多研究使用PQL。
Laplace approximation是比PQL更好一些的方法,其结果接近于真实的ML估计值。Gauss-Hermite quadrature的准确度更高,但是速度比Laplace approximation慢一些;当随机因子超过2各时,就不太适用了。
除此之外,还有基于贝叶斯框架的MCMC方法。

推断Inference
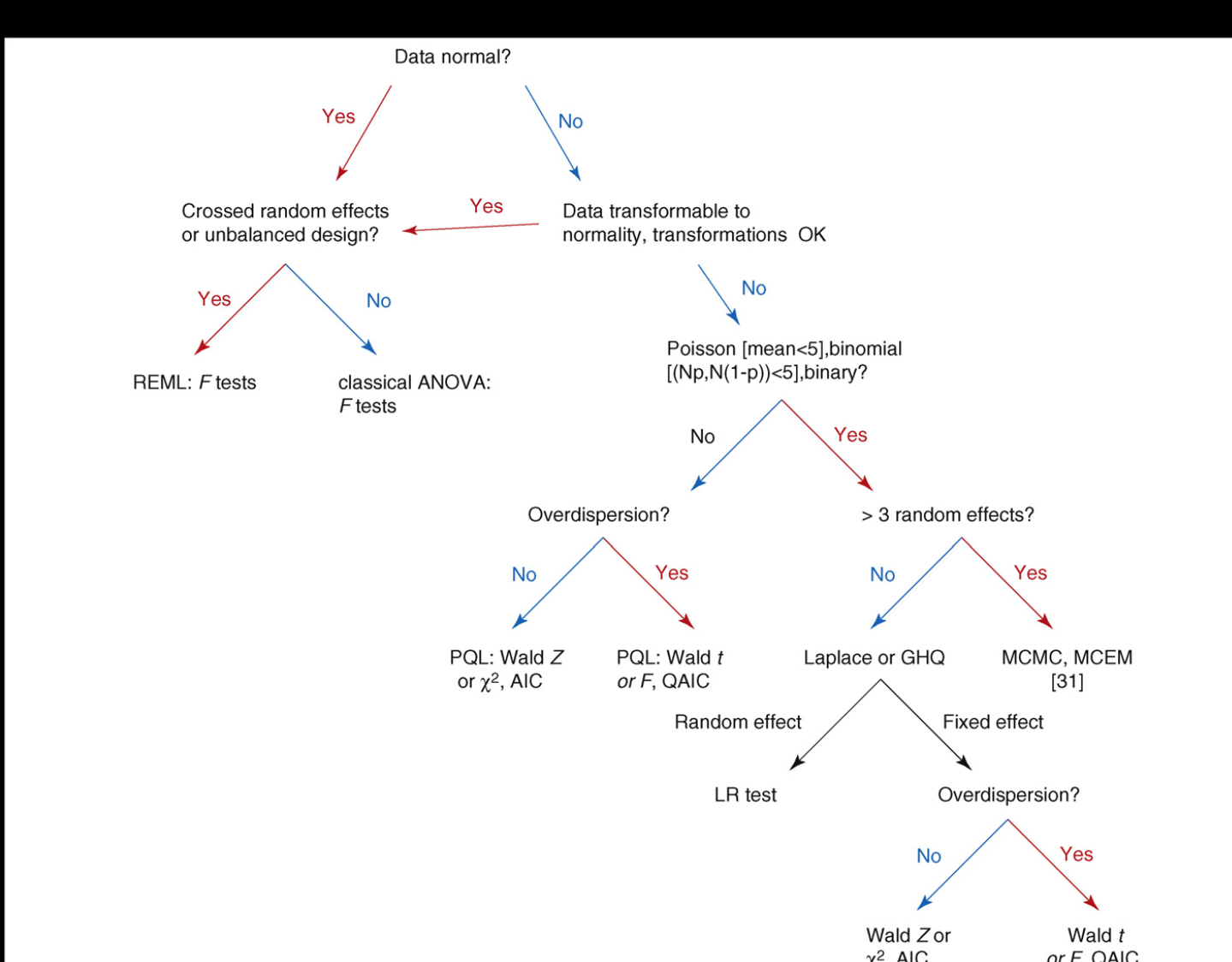
完成第一步的参数估计后,下一步就是进行统计推断。也就是:通过评估估计值及其置信区间、比较并选择最佳模型,从而得到统计学和生物学上的结论。常见的推断有三种:
- 假设检验:频率学派的假设检验来检验统计量,通过p值得判断是否拒绝零假设,如ANOVA中的F检验。
- 模型比较:通过假设检验进行比较,比如比较简单的嵌套模型和更复杂的模型;或者是使用信息论 的方法,即使用预期预测能力的度量来对模型进行排名或对其预测进行平均。
- 贝叶斯方法
假设检验
常见的方法有Wald Z、$X^2$、t检验和F检验 。Wald Z和$X^2$只适用于没有过度离散的GLMM;Wald t 和F检验适用于过度离散的GLMM。不确定性的计算取决于残差自由度的数量,但是呢很难计算。
案例
基因型与环境相互作用在拟南芥对食草动物反应中的作用(genotype-by-environment interaction in the response of Arabidopsis to herbivory)。
数据来源:
响应变量:单株的果实数量,计数型数据,比如1株10个啊20个这种。
选择的模型是Poisson,链接函数是log.
有些处理中果实数量少于5个,因此呢选择Laplace approximation.
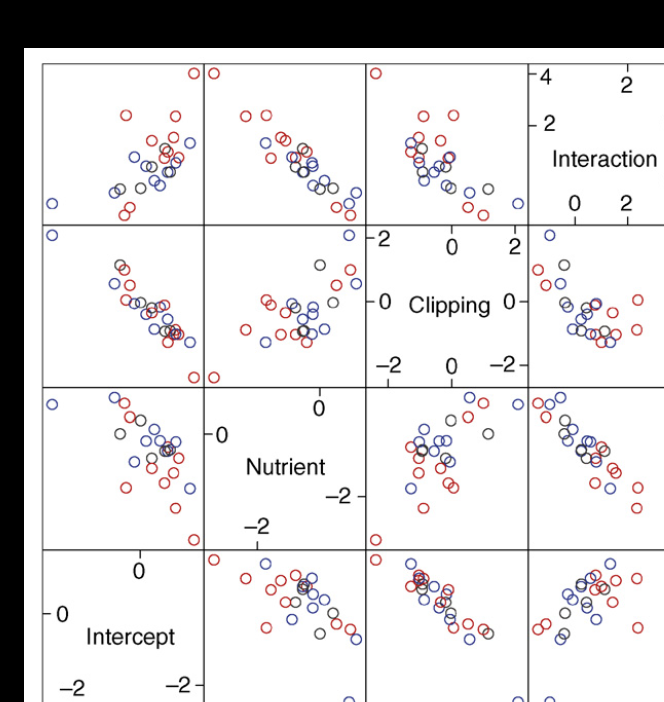
模型使用固定效应:nutrient + clipping + nutrient × clipping.
虽然植株材料来自于三大区域,但是呢考虑到采样个体不够,就忽略了群体结构。
由于残差过度离散,因此使用quasi-Poisson model。